2019.07.29 NEW
文系ビジネスパーソンの必読書! フランスのベストセラー『ぼくと数学の旅に出よう』

売上予測や利益計算、市場分析など、ビジネスに数字はつきものである。また、定性的なものを定量的に捉え直したり、データ群からパターンを抽出し、それをもとに先々の予測を行ったりするような「数学的」な思考のあり方は、複雑さや不確実性が増した社会においてますます重要になってきたといえる。
にもかかわらず、「文系だったせいか、数字や数学的なものは苦手」という人が意外に多いことも事実。そんな方に今回紹介したいのが、「数学嫌いの中高生から文系の大人まで楽しめる」として話題になったフランスのベストセラー、『ぼくと数学の旅に出よう 真理を追い求めた1万年の物語』(NHK出版)だ。
1万年分の「数学の歴史」を凝縮した一冊
本書の著者は1984年生まれのフランス人数学者、ミカエル・ロネー。数学の面白さを世に伝えるべく、青少年向けの数学イベントの開催や数学冒険小説の執筆、動画配信などさまざまな手段で「数学普及活動」に取り組んでいる人物だ。ちなみに、そうした活動が認められ、数学の普及に努める団体や個人に与えられる「ダランベール賞」も受賞している。
本書は、そうした「数学普及活動」の書籍版と呼ぶべき一冊。本国のフランスでは発売とともに話題となり、10万部のベストセラーとなっている。その内容を端的に表すなら「紀元前8000年紀から現在に至るまでの数学的な発見や、思考が深化していく道のりについて、親しみやすい文章で綴った数学史」といったところだ。
“数式まみれの難解な内容ではない”という点がいちばんのポイントで、教科書のような数式や記号の羅列からは決して見えてこない、数学本来の面白さや醍醐味を堪能することができるだろう。
数学は世界を理解するために生まれた抽象的学問
普段から当たり前のものとして使っている「数」。まずは、その概念の誕生を本書から抜粋して見てみよう。
時は紀元前4000年紀のメソポタミア。中東全域に君臨する都市ウルクでは、たくさんの羊が飼われていた。夏には羊たちを街の北部にある餌場へと移動させ、数カ月の間そこで過ごさせる必要があったのだが、羊の飼い主たちに代わって移動と面倒の役割を担っていたのが、羊飼いたちであった。そして、人類最初の「数」は、この飼い主と羊飼いという2者の間で誕生したのだという。
それは次のようなプロセスで進行していった。羊の飼い主は「餌場へ移動・滞在させる前と同じ数の羊を連れ帰ること」を羊飼いに求めた。飼い主たちは、羊飼いが羊を行方不明にさせたり、勝手に物々交換したりすることを恐れていたのだ。
そこで用いられたのが、「トークン」という粘土製のメダルのようなもの。飼い主たちは、羊飼いに羊を預ける前に、羊と同じ数だけの「トークン」を用意して容器に入れておく。そうすれば、羊が戻ってきたときにその数が減っていないかを確認することができた。
しかし、羊飼いの側にしてみればそのやり方にはリスクがあった。自分たちが羊を連れて餌場に滞在している間に、悪意ある飼い主が「トークン」の水増しを行い、羊を連れ帰ったときに「羊の数が足りない」と言いがかりをつけてくるかもしれないからだ。
その防止策として、中が空っぽの粘土玉「ブッラ」に「トークン」を密封して保管するという方法が用いられるようになった。「ブッラ」を壊さないかぎり、「トークン」の数を誤魔化せないようにしたのだ。
やがて「ブッラ」の中にどれだけの「トークン」が入っているかがすぐにわかるように、次のような工夫が行われた。実際に中に入っている「トークン」と同じ分だけ、「トークン」の絵を「ブッラ」の表面に描くようになったのだ。
そこで、誰かがふと気づいた。そもそも、表面に「トークン」の絵が描かれているのであれば、実物の「トークン」が中に入っている必要などないのではないか? かくして、「ブッラ」は平らな粘土板へと姿を変え、「トークン」の代わりに描かれた絵は文字へと進化していった。
そして、紀元前3000年紀頃にはさらに大きな転換が起こる。
それまで、数を表す印は「何を数えるか」によって異なっていた。つまり、8頭の羊は「羊を表す印」を8個描くことで、8頭の牛は「牛を表す印」を8個描くことによって数えられていたのだ。
だがこの頃になると、羊や牛を表す印を頭数分書くのではなく、羊を表す印の後に頭数を示す印を書く、という方法が生み出された。数が数える対象から切り離され、「数自体による数自体のための存在」となったのである(著者はこの瞬間を「数学の誕生」と表現している)。
実際の羊が「トークン」により表され、「トークン」が実体から絵になり、さらなる抽象化が推し進められて数が誕生する――。抽象化によって、現実を効率的かつ正確に理解・把握しようとするという営み、いわば数学的な思考プロセスの始源の光景を追体験してみると、数学は“人間の知恵によって可視化されてきた、実態のないもの”であることがよくわかる。
「優れた抽象的学問、それこそが数学だ。数学者が研究する対象は実体としては存在しないし、分子で構成されたものでもない。単なる考え方にすぎないのだから。ところが、その考え方がこの世界を理解するのに信じられないぐらい役に立つ」(p.38)
著者は数学という学問をこう評しているが、そうした視点を持つだけで、負の数や三角関数、虚数といった概念にも、学生時代ほどの抵抗感を感じなくなるから不思議だ。
「未知」を明らかにしようとした学者たち
一方で、抽象的学問を洗練・深化させ、世界の謎を解き明かしていこうとする数学者たちの探求への意思や、未知へと挑んでいく姿勢もまた、私たちを大いに刺激してくれる。ここで紹介したいのは、17世紀に活躍した数学者たちの活躍だ。
著者によれば、17世紀になると数学者たちは「人間より前から存在していた世界=自然」を解き明かそうという新たな挑戦を始めるようになったのだという(古代からそのような試みはあったが、そこには理論的な根拠は存在しておらず、後にほとんどが間違いだったことが判明している)。
その輝かしい功績の一つとして挙げられるのが、イギリスの科学者アイザック・ニュートン(1642~1727)が発見した万有引力の法則だ。
ニュートンは『プリンキピア(自然哲学の数学的原理)』という著書の中でこう主張した。「地上の物体の落下と空の星の回転は、同じ一つの現象から説明できる」と。ここでいうところの“一つの現象”とは「宇宙の万物は互いに引き寄せ合っている」というもので、この法則は次の公式によって表される。
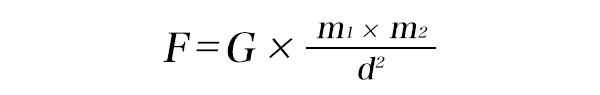
※表記は書籍に準拠
公式の詳細は本書に譲るとして、ここで重要なのは天体の軌道やこの先の変化がこの公式により「計算可能なもの」になったということ。つまり、それまで「神秘的」な現象だった日食や月食が、「神秘的」ではなくなったのだ。何しろ、方程式で未知数の値を求めれば、その発生タイミングを導き出せるようになったのだから。
また、これまで人知の埒外(らちがい)にあったものを解明しようとした動きとしては、確率論も忘れてはならない。時は同じくして17世紀のフランス。科学アカデミーの前身となるパリ・アカデミーという学会で次のような問題が投げかけられたという。
「二人のプレイヤー[1]と[2]が、いくらかの金をかけて3戦先勝方式のゲームに臨んだ。しかしプレイヤー[1]が2対1でリードしたところでゲームは中断。さて、その場合、賭け金はどんなふうに分けたらいいか?」
その日の学会に出席していた二人のフランス人がこの問題に興味を持った。ピエール・ド・フェルマー(生年諸説あり~1665)とブレーズ・パスカル(1623~1662)である。
二人が導き出した答えは「プレイヤー[1]が4分の3、プレイヤー[2]が4分の1」というもの。この分配率は、残りの試合が行われたと仮定した場合にそれぞれのプレイヤーが勝者となる確率に沿ったものである(この計算に自信がなければ本書の251ページを確認されたい)。
二人の後にはスイス人数学者のヤーコプ(ジャック)・ベルヌーイ(1654~1705)が偶然に左右されるゲームの分析を引き継ぎ、はじめて確率論の基本原理を発表することになる。
1枚のコインを連続して10回投げたときに裏が出る回数が4~6回の確率はおよそ66%だが、1,000回投げたときに裏が出る回数が400~600回の確率はおよそ99.99999998%になる。
これは「大数の法則」というもので、たとえ偶然に左右されることであっても、繰り返せば繰り返すほど偶然性が無くなっていくということ――その平均的な結果が予測可能なものになっていくこと――を示すものだった。
その後、数世紀をかけて確率論は洗練を重ね続けており、著者もその一翼を担っている(なお、著者の研究は「偶然性の強化のいくつかのプロセスがときには相互に作用することで起こす変化に関するもの」だそうだ)。
ここでは紹介できなかったが、本書には「フィボナッチ数列」や「円周率」など、数学の不思議さや奥深さを感じられるエピソードも盛りだくさん。1万年にも及ぶ“数学の旅”を終える頃には、数や数学への苦手意識はきれいさっぱり消え去っていることだろう。

■書籍情報
書籍名:ぼくと数学の旅に出よう 真理を追い求めた1万年の物語
著者 :ミカエル・ロネー(Mickaël Launay)
1984年生まれ。数学者。2012年に確率論で博士号を取得。数学の面白さを伝えるために青少年や一般向けのさまざまな活動を行う。2013年にはYouTube動画チャンネル『Michaël Launay』のMicmathsシリーズを開設。2018年現在、150本が配信されている人気サイトとなり、チャンネル登録者数は32万人を超え、アップするたびに数十万から数百万の視聴回数を得ている。著書に、ティーンエイジャー向けの数学冒険小説 L'affaire Olympiaや、52 semaines de défis mathématiquesなどがある。2017年に、本書Le grand roman des maths で《タンジェント賞》を、2018年に、数学の普及に努めた団体や個人に与えられる《ダランベール賞》を受賞。
訳者 :山本 知子(やまもと ともこ)
早稲田大学政治経済学部政治学科卒。東京大学新聞研究所研究課程修了。フランス語翻訳家。訳書に、ベルナール・ヴェルベール『星々の蝶』、ダヴィド・S・シュレベール『がんに効く生活』、ベルナール・アンリ=レヴィ『誰がダニエル・パールを殺したか?』(ともにNHK出版)、ピエール・アスキ『私は勉強したい』(文藝春秋)、アルマン・エルスコヴィシ『数の寓話』(ソニー・マガジンズ)、ソフィー・オドゥワン=マミコニアン『タラ・ダンカン』シリーズ(メディアファクトリー)などがある。
訳者 :川口 明百美(かわぐち あゆみ)
専修大学文学部国文科卒。フランス語翻訳家。訳書に、タニア・クラスニアンスキ『主治医だけが知る権力者』(原書房)、アンヌ=マリー・ポル『フェリシーと夢のトウシューズ』(キノブックス)、共訳書に、カリル・フェレ『マプチェの女』(早川書房)、アラン・セール『ネルソン・マンデラ 差別のない国をめざして』(汐文社)がある。
※本データはこの書籍が刊行された当時に掲載されていたものです。